机器学习三大步骤
先写出一个带有未知参数的数学式
$Function \ with \ Unknown \ Parameters$
$y = b + w x_1$
带有未知参数$b, w$的公式,叫做model(带有未知的参数的数学式)
$x_1:$ 公式中已知的东西叫做feature
$w:$ 不知道的参数叫做weight(权重)
$b:$ 不知道的参数叫做bias (偏移)
根据训练集定义$Loss$
$Loss(b,w)$是一个函数,输入是$b,w$
Loss代表训练出来的函数对于训练集的拟合程度
$Loss: L = \frac{1}{N}\sum\limits_n{e_n} (e = |y - y’|)$ 每项$e$是$model$对于训练集的误差
最佳化
$w^{\star}, b^{\star} = arg \ \min\limits_{w,b}L$
$Gradient\ Descent$
- 随机选取一个初始点$w^0$
- 计算微分 $\frac{\partial L}{\partial w}|_{w= w^0}$
- 根据微分的正负选择向前或向后移动$\eta\frac{\partial L}{\partial w}|_{w= w^0}$, $\eta$学习速率,自己设置
- 迭代的更新$w$值
$model$ 的限制
对于一次项的$model$是一条单纯的斜线,可能无法很好的拟合数据集,这叫做$Model$的$bias$,解决方法,写一个更复杂的,有更多未知参数的$model$
例如需要拟合一个复杂的函数(红色线段), 可以在每次的转折点添加一个蓝色线段,斜率保持相同即可,按理说,越是复杂的红色线段所需要的蓝色线段越多
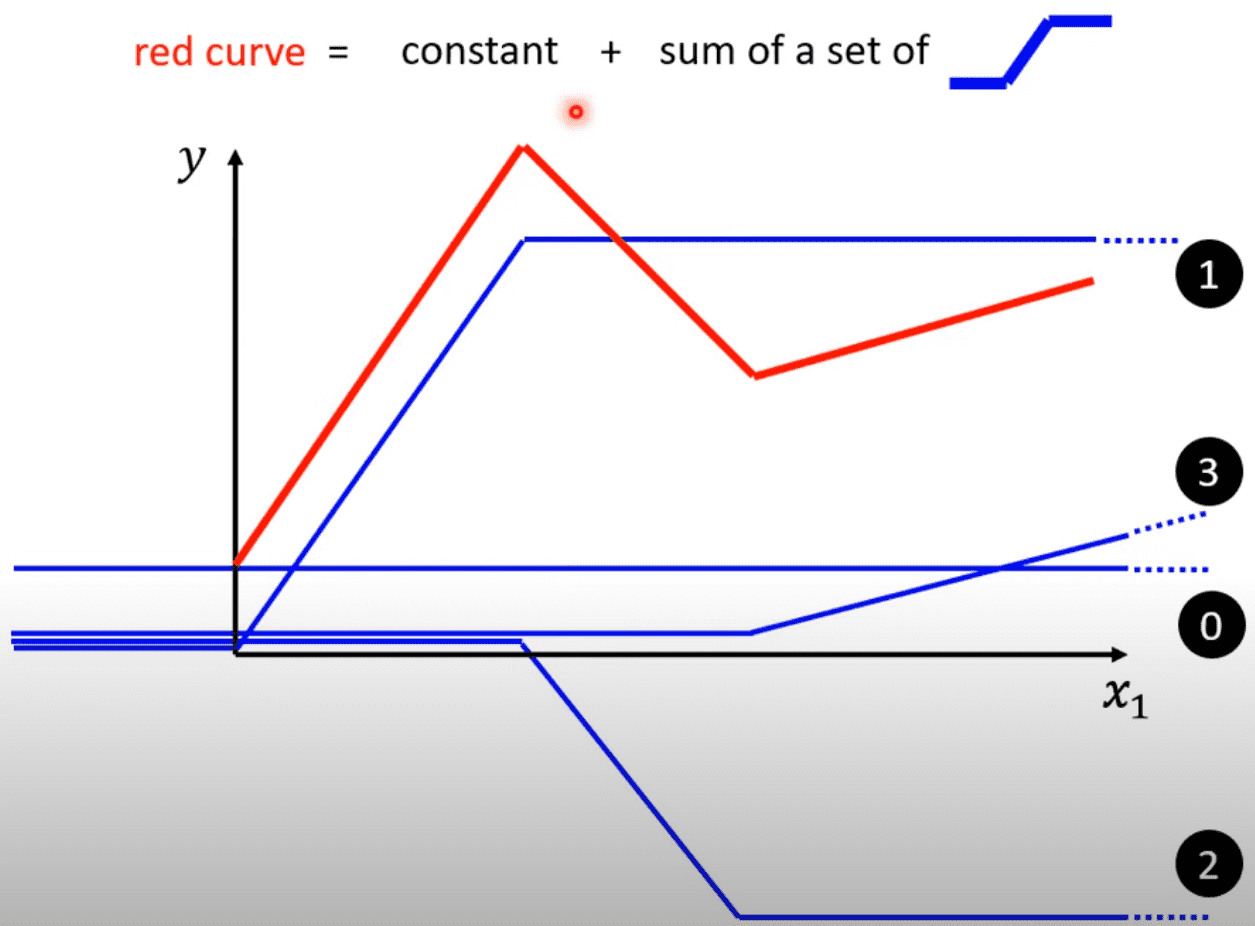
对于连续的曲线可以选择足够多的点,就可以来使用蓝色线段拟合
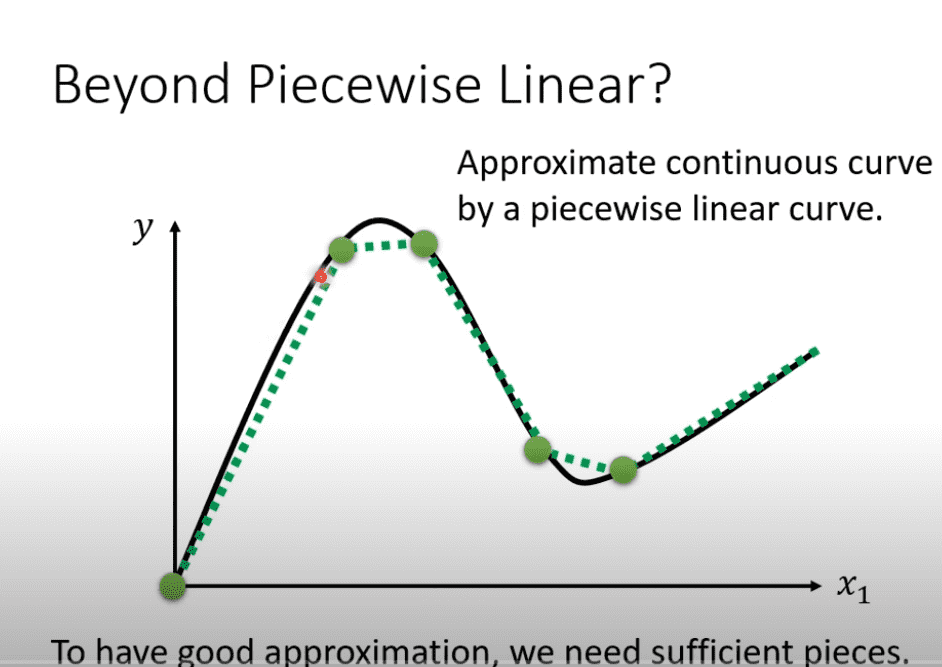
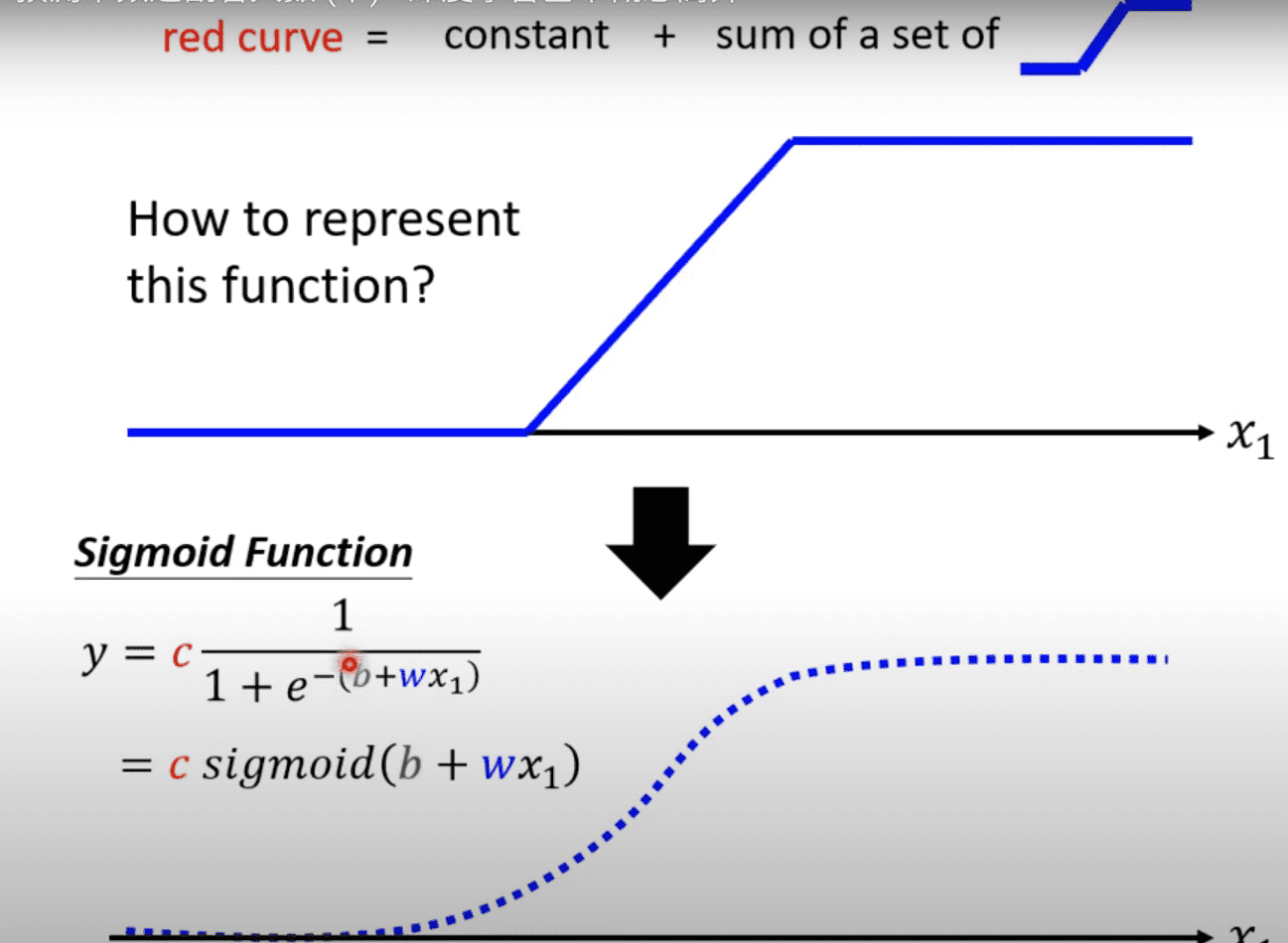
如何来表达蓝色线段
通过一个函数来逼近蓝色线段 $y = c \frac{1}{1 + e ^{-(b+wx_1)}}$ 即 $y = c \ sigmoid (b + wx_1)$
调整$b, w, c$就可以得到各种各样的蓝色线段,改变$w$可以改变斜率,改变$b$会改变偏移,改变$c$会改变高
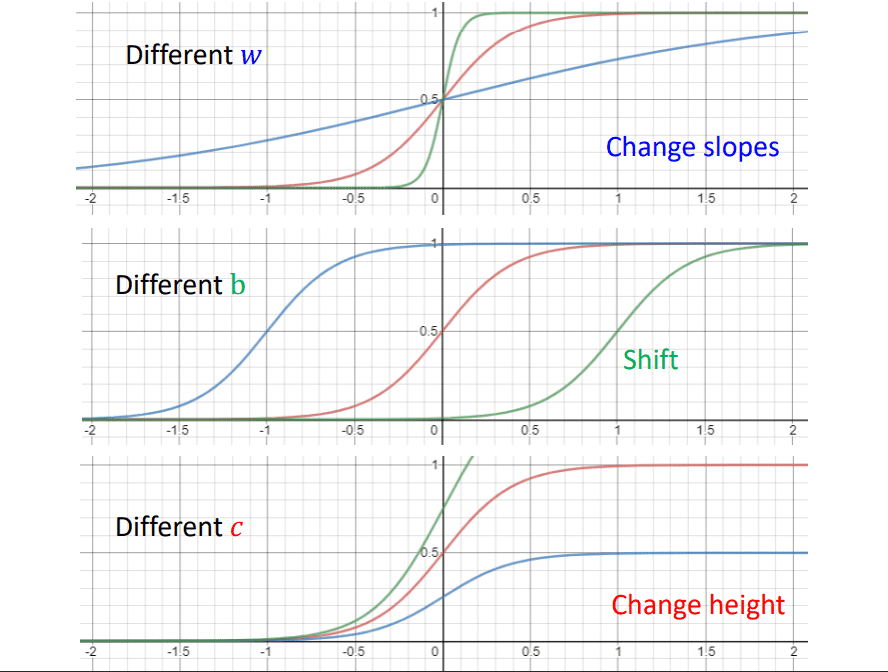
对于不同的蓝色线段使用不同的$b,w,c$来通过$sigmoid$逼近,那么红色线段的函数式就为$y = b + \sum\limits_{i}c_i\ sigmoid(b_i + w_ix_1)$
线性代数表达
对于数据$x_1, x_2, x_3$
$\sum\limits_{i}c_i\ sigmoid(b_i + w_ix_1)$可以表示为
矩阵写法
$r = b + Wx$
在对每一个$r$做$sigmoid$运算 $a = \partial(r)$
红色线段函数: $y = b + \sum\limits_{i}c_i \ a$
使用线性代数表达方式: $y = b + c^T a$
使用$\theta $ 来包含所有的未知参数$\theta = \begin{bmatrix} \theta_1\\ \theta_2 \\ \theta_3 \\ \dots \\ \end{bmatrix}$
$Loss$ 使用$\theta $参数
$Loss$现在使用写成$L(\theta)$
新的$Loss$表示为:$Loss: \ L = \frac{1}{N}\sum\limits_ne_n$
迭代最好的$model$
$\theta^* = arg \ \min\limits_{\theta}L$
随机选择一个初始的$\theta^0$, 对$\theta$的每一项进行微分得到一个向量$g$ ,
$g = \begin{bmatrix} \frac{\partial L}{\partial \theta_1}|_{\theta = \theta^0} \\ \frac{\partial L}{\partial \theta_2}|_{\theta = \theta^0} \\ \frac{\partial L}{\partial \theta_3}|_{\theta = \theta^0} \\ \dots \end{bmatrix}= \nabla L (\theta ^0)$
在$\theta = \theta^0$的位置把所有的参数都对$L$做微分
更新$\theta$的值
$\begin{bmatrix} \theta_1^1 \\ \theta_2^1\\ \dots \end{bmatrix} \longleftarrow \begin{bmatrix} \theta_1^0 \\ \theta_2^0\\ \dots \end{bmatrix} - \begin{bmatrix} \eta \frac{\partial L}{\partial \theta_1}|_{\theta = \theta^0} \\ \eta \frac{\partial L}{\partial \theta_2}|_{\theta = \theta^0} \\ \dots \end{bmatrix}$
新的$\theta$由原先的$\theta^0$ 减去 微分的向量 × $\eta$
$\theta^1 \longleftarrow \theta^0 - \eta g$
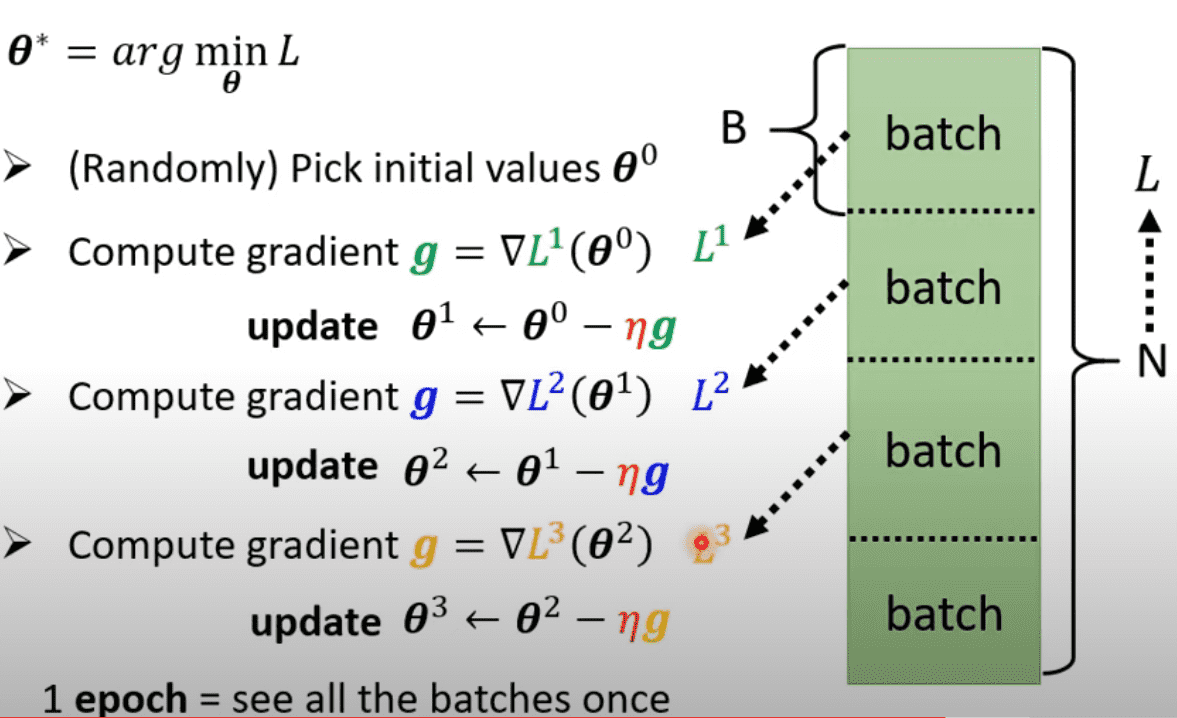
步骤: 先随机选取$\theta^0$,通过计算$gradient$ 得到 $ g = \nabla L (\theta ^0)$,在如此迭代得到$\theta^1, \theta^2,…$直到无法在计算$gradient$时结束
实际操作时,将数据集分为多组,利用每一组来计算$gradient$更新$\theta$
从 $sigmoid$到$RELU$
利用$RELU$来拟合函数 $c\ max(0, b+wx_1)$
$ y = b + \sum\limits_i c_i \ sigmoid(b_i + \sum\limits_jw_{ij}x_j)$
$y = b + \sum\limits_{2i}c_i max(0, b_i+\sum\limits_jw_{ij}x_j)$
$sigmoid$ 和 $RELU$ 统称为$activation\ function$, $RELU$更好一些
过拟合
当拟合的函数次数过多时,对于训练数据会出现拟合效果好,但是对于测试数据拟合率爆炸的情况。



